Exercícios Sobre Produtos Notáveis (Comentados E Resolvidos): Embarque nesta jornada fascinante pelo mundo da álgebra! Desvendaremos os segredos dos produtos notáveis, aquelas fórmulas mágicas que simplificam cálculos complexos e abrem portas para a resolução de problemas aparentemente intransponíveis. Prepare-se para dominar o quadrado da soma, o quadrado da diferença e o produto da soma pela diferença, aplicando-os em exercícios cuidadosamente selecionados, desde os mais básicos até os desafios que exigem raciocínio estratégico.
Cada passo será detalhado, cada solução comentada, guiando você rumo à maestria algébrica.
Através de exemplos práticos e contextualizados, você verá como esses conceitos transcendem o universo abstrato da matemática, encontrando aplicações em diversas áreas, como física, engenharia e até mesmo no dia a dia. Aprenderá a fatorar expressões, resolver equações e dominar técnicas que simplificarão seus estudos e lhe proporcionarão uma compreensão profunda e duradoura dos produtos notáveis. Prepare-se para uma experiência enriquecedora e transformadora!
Produtos Notáveis: Exercícios Sobre Produtos Notáveis (Comentados E Resolvidos)

Embarque conosco nessa jornada fascinante pelo mundo dos produtos notáveis! Eles são ferramentas matemáticas poderosas, capazes de simplificar cálculos complexos e revelar a elegância da álgebra. Dominá-los é abrir a porta para uma compreensão mais profunda da matemática e suas aplicações no dia a dia. Prepare-se para desvendar seus segredos!
Produtos Notáveis: Conceitos e Fórmulas

Os produtos notáveis são expressões algébricas que, devido à sua estrutura particular, permitem um cálculo mais rápido e eficiente do que a multiplicação direta dos termos. Três deles são fundamentais: o quadrado da soma, o quadrado da diferença e o produto da soma pela diferença. Cada um possui uma fórmula específica, derivada da propriedade distributiva da multiplicação, que facilita a obtenção do resultado final.
Vamos explorar cada um deles individualmente.
Quadrado da Soma
O quadrado da soma de dois termos (a + b)² é uma expressão que representa a multiplicação de (a + b) por si mesmo. A fórmula para o quadrado da soma é:
(a + b)² = a² + 2ab + b²
. Isso significa que o resultado é a soma dos quadrados dos dois termos (a² e b²) mais o dobro do produto dos dois termos (2ab).Exemplo numérico: (3 + 5)² = 3² + 2(3)(5) + 5² = 9 + 30 + 25 = 64. Observe que (3+5)² = 8² = 64, confirmando a fórmula.Aplicação prática: Imagine que você precisa calcular a área de um quadrado cujo lado mede (x + 2) metros.
Utilizando o quadrado da soma, a área será (x + 2)² = x² + 4x + 4 metros quadrados. Se x = 3 metros, a área será 3² + 4(3) + 4 = 25 metros quadrados.
Quadrado da Diferença
Similarmente ao quadrado da soma, o quadrado da diferença de dois termos (a – b)² representa a multiplicação de (a – b) por si mesmo. Sua fórmula é:
(a – b)² = a²2ab + b²
. Note que a única diferença em relação ao quadrado da soma é o sinal do termo 2ab, que agora é negativo.Exemplo numérico: (7 – 2)² = 7²2(7)(2) + 2² = 49 – 28 + 4 = 25. Novamente, (7-2)² = 5² = 25, validando a fórmula.Aplicação prática: Considere a construção de um jardim quadrado com lado (y – 1) metros.
A área do jardim será (y – 1)² = y²
- 2y + 1 metros quadrados. Se y = 5 metros, a área será 5²
- 2(5) + 1 = 16 metros quadrados.
Produto da Soma pela Diferença

Este produto notável envolve a multiplicação de dois binômios, um representando a soma de dois termos (a + b) e o outro, a diferença dos mesmos termos (a – b). A fórmula é surpreendentemente simples:
(a + b)(a – b) = a²b²
. O resultado é a diferença dos quadrados dos dois termos.Exemplo numérico: (6 + 4)(6 – 4) = 6²
- 4² = 36 – 16 = 20. Observe que (6+4)(6-4) = 10
- 2 = 20, confirmando a fórmula.
Aplicação prática: Imagine que você precisa calcular a área de um retângulo com comprimento (x + y) e largura (x – y). Usando o produto da soma pela diferença, a área será (x + y)(x – y) = x²
- y² unidades de área. Se x = 10 e y = 3, a área será 10²
- 3² = 91 unidades de área.
Comparação dos Três Produtos Notáveis

A tabela a seguir resume as fórmulas, exemplos e observações sobre os três produtos notáveis:
| Produto Notável | Fórmula | Exemplo Resolvido | Observação |
|---|---|---|---|
| Quadrado da Soma | (a + b)² = a² + 2ab + b² | (2 + 3)² = 2² + 2(2)(3) + 3² = 25 | O resultado sempre é um trinômio quadrado perfeito. |
| Quadrado da Diferença | (a – b)² = a²
|
(5 – 1)² = 5² – 2(5)(1) + 1² = 16 | O resultado sempre é um trinômio quadrado perfeito. |
| Produto da Soma pela Diferença | (a + b)(a – b) = a² – b² | (4 + 2)(4 – 2) = 4² – 2² = 12 | O resultado sempre é uma diferença de quadrados. |
Exercícios Resolvidos
Embarque conosco nesta jornada de descoberta e domínio dos produtos notáveis! Resolver exercícios é a chave para internalizar os conceitos e desenvolver a fluência algébrica necessária para enfrentar desafios mais complexos. Através de exemplos cuidadosamente selecionados, de diferentes níveis de dificuldade, vamos desvendar o poder e a elegância desses atalhos matemáticos.
Prepare-se para aprimorar suas habilidades e desfrutar da satisfação de solucionar problemas com precisão e eficiência.
Exercícios Resolvidos com Diferentes Níveis de Complexidade, Exercícios Sobre Produtos Notáveis (Comentados E Resolvidos)
A prática constante é fundamental para o aprendizado eficaz. Os exercícios a seguir, progressivamente mais desafiadores, irão consolidar seu conhecimento sobre os três produtos notáveis: quadrado da soma, quadrado da diferença e produto da soma pela diferença. Cada passo da resolução será detalhado, permitindo uma compreensão completa do processo.
- (Fácil) (x + 2)²
- Utilizamos a fórmula do quadrado da soma: (a + b)² = a² + 2ab + b²
- Identificamos a = x e b = 2.
- Substituindo na fórmula: (x + 2)² = x² + 2(x)(2) + 2² = x² + 4x + 4
- (Médio) (3y – 5)²
- Aplicamos a fórmula do quadrado da diferença: (a – b)² = a²
-2ab + b² - Neste caso, a = 3y e b = 5.
- Substituindo: (3y – 5)² = (3y)²
-2(3y)(5) + 5² = 9y²
-30y + 25 - (Médio) (2a + b)(2a – b)
- Reconhecemos o produto da soma pela diferença: (a + b)(a – b) = a²
-b² - Aqui, a = 2a e b = b.
- Aplicando a fórmula: (2a + b)(2a – b) = (2a)²
-b² = 4a²
-b² - (Difícil) (x + 2y)³
- Apesar de não ser um produto notável básico, podemos expandir utilizando o binômio de Newton ou a multiplicação direta.
- Utilizando a multiplicação direta: (x + 2y)(x + 2y)(x + 2y) = (x² + 4xy + 4y²)(x + 2y) = x³ + 6x²y + 12xy² + 8y³
- (Difícil) (4m² – 9n²)
- Podemos fatorar essa expressão reconhecendo a diferença de quadrados: a²
-b² = (a + b)(a – b) - Neste caso, a = 2m e b = 3n.
- Portanto, (4m²
-9n²) = (2m + 3n)(2m – 3n)
Exercício Combinando Produtos Notáveis
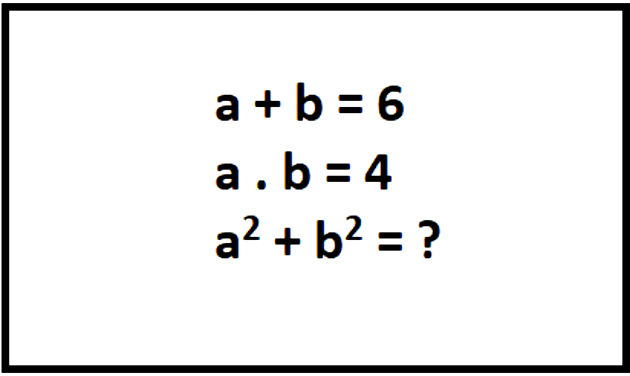
Resolva a expressão: (x + 1)²
(x – 1)²
Para resolver essa expressão, primeiramente desenvolvemos cada quadrado utilizando as fórmulas dos produtos notáveis. Em seguida, simplificamos a expressão resultante combinando termos semelhantes.
- Desenvolvendo (x + 1)²: x² + 2x + 1
- Desenvolvendo (x – 1)²: x² – 2x + 1
- Subtraindo a segunda expressão da primeira: (x² + 2x + 1)
- (x²
- 2x + 1) = x² + 2x + 1 – x² + 2x – 1 = 4x
Simplificação de Expressões Algébricas Utilizando Produtos Notáveis
Os produtos notáveis são ferramentas poderosas para simplificar expressões algébricas complexas, tornando-as mais concisas e fáceis de manipular.
- Exemplo 1 (Binômios): Simplifique (a + b)(a – b) + 2ab. Utilizando o produto da soma pela diferença, temos a²
b² + 2ab.
- Exemplo 2 (Monômios e Binômios): Simplifique 2x(x + 3)²
4x³. Primeiro, desenvolvemos o quadrado do binômio
2x(x² + 6x + 9)
4x³ = 2x³ + 12x² + 18x – 4x³ = -2x³ + 12x² + 18x.
- Exemplo 3 (Trinômios): A simplificação de expressões com trinômios muitas vezes requer o uso de fatoração antes da aplicação de produtos notáveis, dependendo da estrutura da expressão.

